这位插画大师叫莫里茨·科内利斯·埃舍尔(Maurits Cornelis Escher,1898~1972)。
埃舍尔当时身处欧洲的动荡年代,也是欧洲大师频现的时代,比如毕加索、莫迪利亚尼、席勒.....都出现在这段时期。难道是因为这些大师的光芒将其掩盖了吗?还是他的作品真的就是无法评定?
① 《观景楼》
这是是埃舍尔的代表作品之一。乍一看,画面和谐而静谧。
仔细看的话,你会发现观景楼的二层和三层竟然一个是纵向、一个是横向,并且支撑楼面的石柱也是交错的,显然,这在现实中是不可能存在的。
更有意思的是,处于画面边缘左下角的男孩手中的“玩具”——立方体,这也是一个不可能的立方体。
这个立方体就是最早的“不可能图形”( impossible figure ),这类图形是人类视觉对一个二维图形进行三维投射时形成的光学错觉,它在三维空间中不可能存在。这类奇幻的不可能场景,在埃舍尔的作品中随处可见。

② 《升与降》
作品《升与降》中,楼顶分别有两队教士,一路向上走,一路向下行,到底是谁升谁降呢?很难判断,也不需要做出判断,因为他们最终都是在相近的平面上打转。
这种视错觉带来的感观体验令人着迷,只要站在他的作品前,每一幅都可以使人长久驻足。但埃舍尔又不只是在塑造“不可能图形”,他总是试图在不起眼的角落里注入自己的观点:中画面左侧的中间层有一位悠闲的观察者,在平静地看着楼上发生的一切;而画面下方的一位,则是在等待更多的“打转者”。

③ 《高与低》
埃舍尔这种诡异的空间布局,使得同时代的人称他为“巫师”。其好友布鲁诺·恩斯特在认识埃舍尔之前心怀忐忑:“我还真是有些犹豫,因为在我看来,埃舍尔不仅是一位伟大的艺术家,更是一个巫师。”
恩斯特说自己曾连续好几年观察石版画《高与低》,自己越是投入,就越感觉怪异,而且有一种说不上的魔力来把他深深吸引住,他甚至要强迫自己不去看这幅画。

④ 《瀑布》
《瀑布》是埃舍尔最为人所知的作品之一,图中的瀑布会源源不断地落下,水落下的水又逆流而上,荒唐至,但又会让你百看不腻。画面下方还有一位饶有兴致的观察者,似乎他没发现什么不对劲儿。此时,他既是画外的观看者,也是埃舍尔自己。
《纪念碑谷》的制作人 Ken Wong 曾说,正是埃舍尔的名作《瀑布》给了他们灵感才制作出这款游戏。

⑤ 《美洲鳄》
埃舍尔不仅是个艺术家,还是个哲学家。美洲鳄从封面上爬出来,转了一个圈又爬回去了。这种二维到三维的反复转变,似乎在思考我们的宇宙空间;也似乎在问道:我们来自哪里,我们又要往哪儿去?

⑥ 《静物和街景》
埃舍尔巧妙地将自己的书桌跟窗前的街景融合到了一起,我们的视线随着弯曲的街道延伸至远方。这到底是书桌还是远方?在某种意义上,书=知识,书桌=学习知识的地方;学习知识才能寻找诗和远方。

⑦ 《骑士》
可以看得出,埃舍尔的作品注入了太多理性,尤其是一些数学元素,所以曾遭到当时艺术界的排挤。也正因如此,他的作品在科学界却引起了极大的反响。因为不仅可以从他的画中看到对分形、对称、双曲几何、多面体、拓扑学等数学概念的形象表达,还可以从中体会到他那充满哲学的思考精神。
这些违背现实规律、超现实的场景,在埃舍尔的作品中能十分自然和谐地展示,这就是埃舍尔的魔力。而这股魔力还蔓延到了物理界,其中物理学家杨振宁曾将埃舍尔的作品写进了他的著作《基本粒子及其相互作用》中。而他的著作《基本粒子发现简史》的封面便是《骑士》。

⑧ 《手与反射球体》
连自画像都那么有个性......
1935年,埃舍尔开始迷恋球体,作品《手与反射球体》是他透过水晶球的自画像,此后我们可以不时看见水晶球在他的画面上出现。水晶球的神秘似乎给了埃舍尔魔幻的力量,手持水晶球的埃舍尔更像巫师了......

⑨ 《阳台》
密集的建筑被球形扭曲,而中间还有令人迷醉的大麻,这种视觉的变形会使你陷入迷幻状态。这种“致幻”作用深得60年代的嬉皮士们喜爱。
其中著名的滚石乐队主唱米克·贾格尔( Mick Jagger )曾写信给埃舍尔,希望在乐队专辑《 Through the Past Darkly 》封面印上一幅他的作品,结果遭到了不喜欢通俗文化的埃舍尔的拒绝。
滚石乐队成员
而面对科学家对自己作品的欣赏,埃舍尔的态度却截然相反。英国的著名数学家Coxeter有一次想在自己的文章中加入埃舍尔的一幅画,征求其同意,埃舍尔便喜出望外地答应了!
如果你仔细观看《阳台》,画面中央被放大的植物大麻就会直接抓住你的视线,大脑可能变得一片空白,你只想出神地盯着这个凸起的幻象。据说黑白反反差的效果更佳。

⑩ 《莫比乌斯环》Ⅰ、Ⅱ

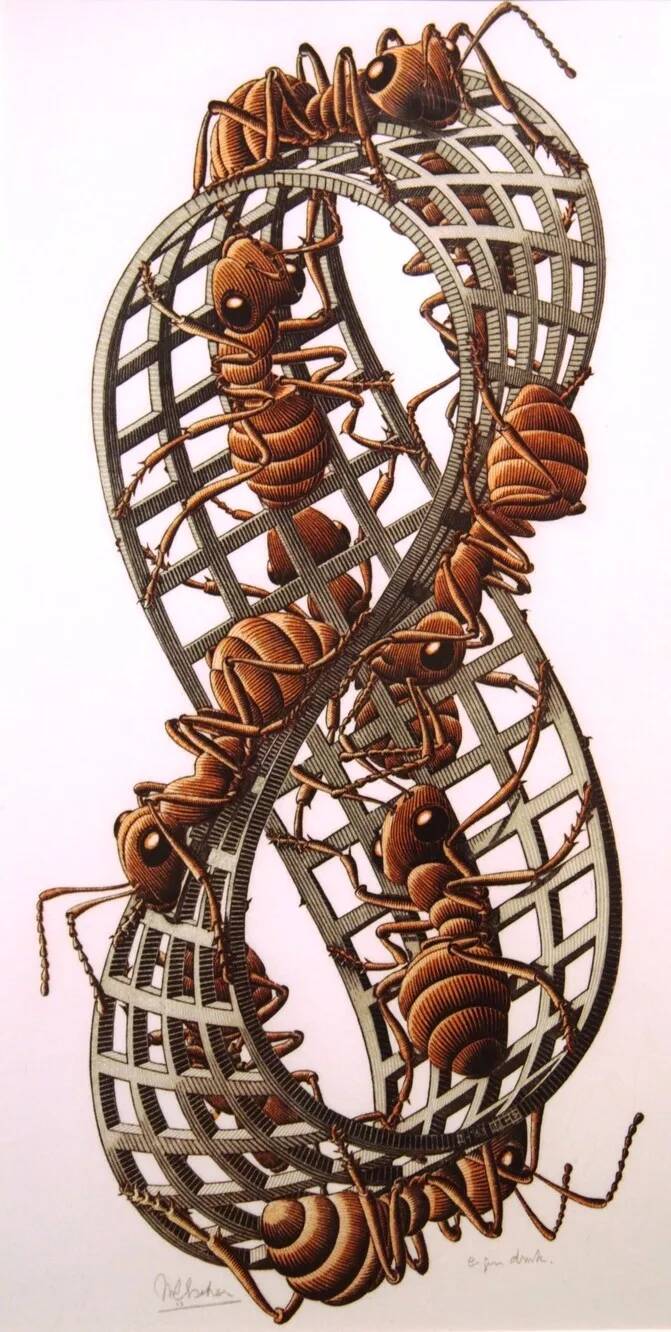
有一回,一位数学家告诉埃舍尔,有一位德国数学家叫莫比乌斯发现:把一根纸条扭转180°后两头再粘接起来做成的纸带圈(后称为“莫比乌斯环”),具有魔术般的性质。埃舍尔后来对儿子说,他觉得自己心里就有一个莫比乌斯带,自己的眼睛正是和外面的世界进行着莫比乌斯般扭曲纠缠。后来他创作了一幅作品,上面的蚂蚁在莫比乌斯带上无休止地爬行。埃舍尔对数学有种本能的理解,很多深奥的数学问题他都能领会,他还可以通过画笔将很多抽象的数学概念赋予了灵魂、生命。很多数学教授都认为埃舍尔的一些画作对教学上有很大的帮助。
埃舍尔逝世于 1972 年,他的个性和作品都很平和。不是梵·高式的悲情艺术家,也没有毕加索在世时的风光。
值得高兴的是,艺术史学家贡布里希在 1987 年出版的《艺术与错觉:图画再现的心理学》中,以埃舍尔的绘画为例探讨了观看行为与绘画的关系,为埃舍尔的绘画找到了艺术史上的地位:
埃舍尔绘画的特征在于利用空间扭曲与正负形转化来造成视错觉。20 世纪以前的很多绘画都是在二维平面上构造三维的空间效果,从而让观者产生“身临其境”、达到“欺骗眼睛”的效果,绘画如同照相式的描摹,这类绘画可以被称为再现性绘画。当我们面对这些绘画时,可以不假思索地识别出画中画的是盘子、杯子等等。而埃舍尔的画破坏的正是我们对再现的简单认识。
古代哲学家毕达哥拉斯就认为世界就是由数来组成的,以前我对这句话百思不得其解。如今,经过埃舍尔的“解释”后,我似乎又懂了一点。
更多埃舍尔的作品欣赏。
电影《盗梦空间》(2010年)中的某些情景,便是对埃舍尔大师的致敬。
素材源于网络 | 侵删!